목차
DFS 는 해당 시작 정점에서 갈 수 있는 모든 정점을 깊이 우선으로 방문한 뒤 종료된다!
깊이 우선 탐색이란?
Depth First Search, 흔히 줄여서 DFS 라고 부른다.
트리
나
그래프
에서 한 루트로 탐색하다가 최대한 깊숙히 탐색한 뒤 다시 돌아가 다른 루트를 탐색하는 방법이다. 대표적으로 백트래킹에 사용한다. 일반적으로 두 가지의 구현 방법이 있는데, Stack 을 이용한 구현 방법과 재귀호출을 사용한 구현 방법이다.
DFS 의 구현 방법 - 재귀 호출을 이용한 구현
//재귀 호출을 이용한 dfs 의 구현
fun dfs(to: Int, visited: Array<Boolean>, adjacentList: Array<ArrayList<Int>>) {
visited[to] = true // -> 현재 정점에 대한 방문 처리
println("$to ${if (adjacentList[to].isEmpty()) "나는 리프노드입니다!" else ""}") //-> 탐색 순서를 출력
//만약 다음 노드를 방문하지 않았다면, 다음 노드 방문
for (goTo in adjacentList[to]) {
if (!visited[goTo]) {
dfs(goTo, visited, adjacentList)
}
}
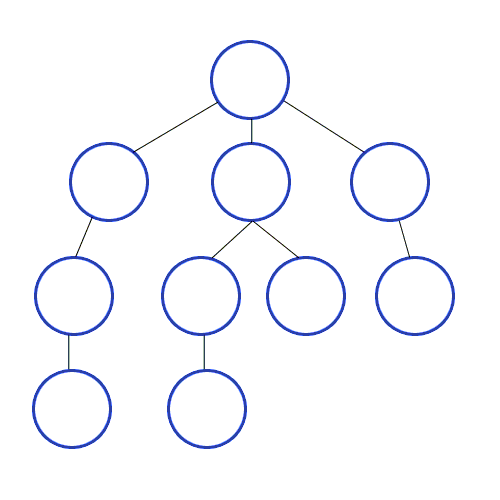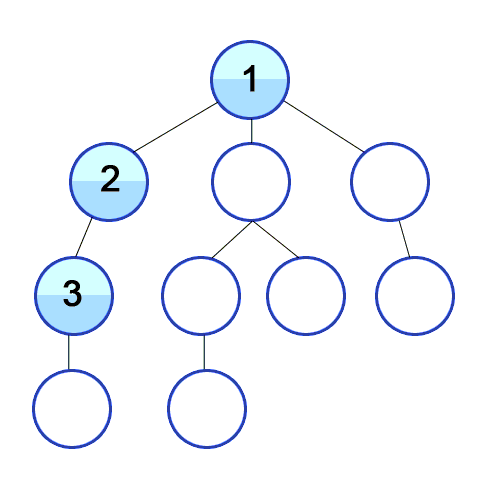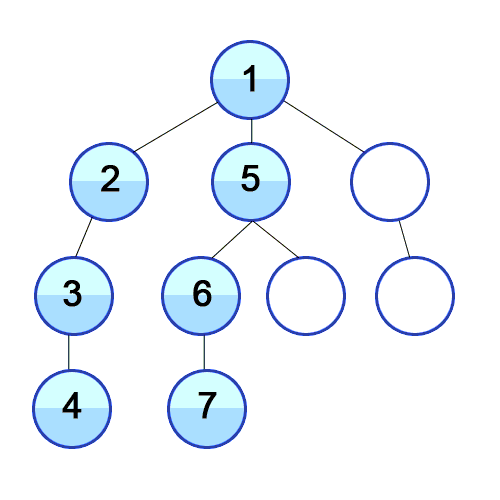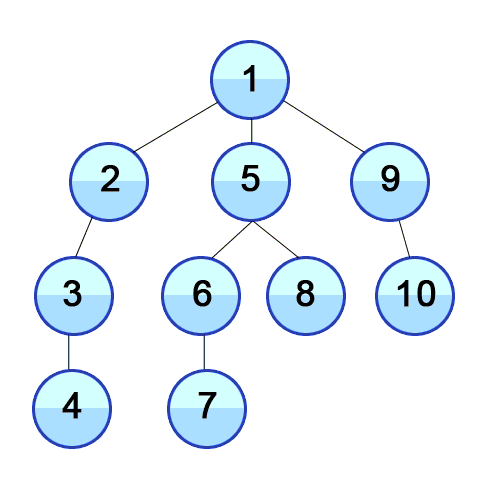
}위의 재귀호출을 이용해 구현한 dfs 알고리즘을 가지고 다음과 같은 그래프를 탐색해보자!
그렇다면 결과는 다음과 같이 나온다. 일부러 순서대로 나오게 정점의 번호를 조정하였다.
1
2
3 나는 리프노드입니다!
4 나는 리프노드입니다!
5
6 나는 리프노드입니다!
7
8 나는 리프노드입니다!
9
10
11 나는 리프노드입니다!
12 나는 리프노드입니다!
13 나는 리프노드입니다!DFS의 구현 방법 - 스택을 이용한 구현
그렇다면 이번엔 Stack 자료구조를 이용해서 dfs 를 구현해보자!
fun stackDfs(start: Int, adjacentList: Array<ArrayList<Int>>) {
val visited = Array(14) { false }
visited[start] = true;
val stack = Stack<Int>()
stack.add(start)
while (!stack.isEmpty()) {
val to = stack.pop()
println("$to ${if (adjacentList[to].isEmpty()) "나는 리프노드입니다!" else ""}") //-> 탐색 순서를 출력
for (goTo in adjacentList[to]) {
if (!visited[goTo]) {
visited[goTo] = true
stack.add(goTo)
}
}
}
}해당 알고리즘으로 위의 그래프를 탐색한 결과는 다음과 같다.
1
9
13 나는 리프노드입니다!
10
12 나는 리프노드입니다!
11 나는 리프노드입니다!
5
7
8 나는 리프노드입니다!
6 나는 리프노드입니다!
2
4 나는 리프노드입니다!
3 나는 리프노드입니다!이전과는 순서가 다르게 나온 것을 확인할 수 있다. 재귀 호출을 이용한 dfs 는 다음 노드를 바로 방문하지만, Stack 을 이용한 dfs는 다음에 방문할 수 있는 노드를 모두 Stack 에 추가한 뒤 다음 노드를 방문하기 때문에 이렇게 다른 결과가 나오는 것이다. 그러나 탐색 순서를 그래프와 비교하면, 이 역시 깊이를 우선으로 하여 탐색한 사실을 알 수 있다.
다른 것은 그래프의 좌측을 먼저 탐색하느냐 우측을 먼저 탐색하느냐 뿐이다.
그렇다면 DFS 의 시간 복잡도는 어떻게 될까? DFS 를 이용해 탐색할 그래프의 정점의 개수를 V, 간선의 개수를 E 라고 하면, 시간 복잡도는O(V+E)O(V+E)O(V+E) 가 된다.
사실 위와 같은 그래프의 탐색은 매우 단순하므로, 실제 알고리즘 문제를 해결할 때는 이를 응용할 수 있어야 한다. 이후 내용에서는 DFS 를 이용한 Cycle 탐색의 방법을 설명해보겠다.
DFS 를 활용한 사이클 탐색 방법
방향 그래프에서 사이클이란 특정 정점에서 시작해 어떠한 경로를 지나 다시 그 정점으로 돌아오는 경로를 말한다.
무방향 그래프
에선 서로소 집합을 활용해 사이클의 존재 여부를 쉽게 판별할 수 있다. 그러나 방향 그래프에선 어떻게 사이클이 있는지 판별할까?
DFS 를 활용하여 사이클을 판별할 수 있을지 고민해보자! !! !! ! !! ! !

사이클 존재 유향 그래프
가장 단순하게 생각해보자. 어떤 정점에서 DFS 를 시작했을 때, 해당 탐색에서 자기 자신으로 돌아온다면, 사이클이 존재한다고 판별할 수 있다. 예를 들어 1에서 시작하는 DFS 는 다시 시작점인 1로 돌아오지 못하기 때문에, 1을 거쳐가는 사이클이 없지만, 6에서 시작하는 DFS 는 다시 6으로 돌아오기 때문에 6을 거쳐가는 사이클은 존재한다고 생각할 수 있다.
따라서 이 경우엔 1에서 시작하는 DFS를 돌려보고, 2에서 시작하는 DFS를 돌려보고,.... 7에서 시작하는 DFS 를 돌리는 형식이다. 이전에 DFS 의 시간 복잡도는O(V+E)O(V+E)O(V+E) 라 하였는데, 이 방법을 이용하면 모든 정점 V개에 대해 DFS 를 돌리기 때문에 시간 복잡도는O(V∗(V+E))O(V * (V+E))O(V∗(V+E)) 라고 할 수 있다.
그렇다면 모든 정점에 대해 사이클을 찾지 않고 한 번의 DFS 로 사이클을 찾는 방법이 있을까? DFS 의 정의를 한 번 생각해보자
DFS 는 해당 시작 정점에서 갈 수 있는 모든 정점을 깊이 우선으로 방문한 뒤 종료된다!
즉 어떤 정점에서 시작하는 모든 길에 대한 DFS 탐색이 종료되지 않았는데, 다시 해당 정점을 방문하게 된다면 사이클이 존재한다고 판별할 수 있다.
위의 유향 그래프를 예로 들자면, 6에서 시작하는 모든 탐색이 종료되기 전에, 7이 6을 방문하므로 사이클이 존재한다고 할 수 있고, 이것은 DFS 를 탐색하며 따로 현재 깊이에 대한 방문 배열을 선언하여 탐지할 수 있다.
다음과 같은 코드를 살펴보자
fun dfs(to: Int, visited: Array<Boolean>, adjacentList: Array<ArrayList<Int>>, visitStack: Array<Boolean>) {
visited[to] = true // -> 현재 정점에 대한 방문 처리
visitStack[to] = true // -> 현재 탐색 루트에서 해당 정점을 방문 처리 만약 이 정점에서 시작하는 탐색이 모두 끝나면 다시 false 로 변경
println("$to ${if (adjacentList[to].isEmpty()) "나는 리프노드입니다!" else ""}") //-> 탐색 순서를 출력
//만약 다음 노드를 방문하지 않았다면, 다음 노드 방문
for (goTo in adjacentList[to]) {
if (!visited[goTo]) {
dfs(goTo, visited, adjacentList, visitStack)
} else if (visitStack[goTo]) {
println("$goTo 를 향한 Cycle 이 발생함!")
}
}
visitStack[to] = false // -> 현재 정점에서 시작한 탐색이 모두 끝났으므로, 방문 여부를 다시 false 로 변경
}해당 코드에 대한 탐색 순서는 다음과 같이 나온다
1
2
3
4
7
6
4 를 향한 Cycle 이 발생함!
5기존 DFS 알고리즘과 다른 점은, visitStack 이라는 배열을 따로 선언하고, 해당 배열에 대한 방문 처리를 한다는 점이다. 이 visitStack은 해당 정점에서 시작하는 모든 탐색이 끝난 뒤에 다시 false로 변경되는데, false 가 되기 전 다시 이 정점을 방문하게 되면, 해당 정점을 향한 사이클이 존재한다는 뜻이다.
따라서 단 한번의 DFS 탐색으로 사이클의 존재를 찾을 수 있다.
다음과 같은 그래프를 가지고 다시 한 번 탐색을 돌려보자
우리가 대충 눈으로 봤을 때, 7-9-8-7 로 이어지는 사이클과 4-11-12-10-4 로 이어지는 사이클이 존재하는 것을 알 수 있다.
위의 코드를 다시 한 번 돌리면 아래의 결과가 나온다.
1
2
5 나는 리프노드입니다!
6 나는 리프노드입니다!
3
7
9
8
7 를 향한 Cycle 이 발생함!
4
11
12
10
4 를 향한 Cycle 이 발생함!정확한 결과가 나오는 것을 확인할 수 있다. 7에서 탐색을 시작할 때 visitStack[7]이 true 가 되고, 7에서 시작하는 탐색이 끝나기 전 8에서 7을 방문했으므로 사이클이 존재한다고 판별했다. 4에서 시작하는 사이클도 이와 마찬가지의 방법으로 탐지하는 것을 알 수 있다.
DFS 를 이용한 유향 그래프 사이클 탐색 문제 추천
다음 문제들은 DFS 를 이용한 사이클 탐지 기법이 활용되는 문제들이다.




Comment