알고리즘
자료구조 - 힙 (Heap) java
호종이
2022. 2. 4. 11:37
우선순위 큐란?
- 자료가 들어오는 순서와 상관없이, 우선순위가 제일 높은 데이터가 먼저 빠져나간다
- 우선순위 큐의 활용사례
- 네트워크 트래픽 제어
- 운영 체제에서 프로세스 스케줄링
- 시뮬레이션
| 자료구조 | 삭제되는 데이터 |
| 스택(Stack) | 가장 최근에 들어온 데이터 (Last In First Out) |
| 큐(Queue) | 가장 먼저 들어온 데이터 (First In First Out) |
| 우선순위 큐(Queue) | 우선순위가 제일 높은 데이터 |
힙이란?
- 완전 이진 트리로, 우선순위 큐를 위하여 만들어진 자료구조이다.
- 우선순위가 제일 높은 데이터를 바로 찾아내도록 만들어진 자료구조다
- 힙은 일종의 반정렬 상태를 유지한다.
- 우선순위가 제일 높은 값이 루트 노드에 존재한다.
- 부모 노드가 자식 노드보다 우선순위가 높지만, 완전히 정렬된 상태는 아니다
힙의 종류
- 최대 힙(max heap)
- 부모 노드의 키 값이 자식노드보다 크거나 같은 완전 이진 트리
- 최상위 루트 노드엔 항상 제일 큰 값이 존재한다.

- 최소 힙(min heap)
- 부모 노드의 키 값이 자식노드보다 작거나 같은 완전 이진 트리
- 최상위 루트 노드엔 항상 제일 작은 값이 존재한다

힙의 삽입 연산 - 시간 복잡도 (log N)
- 힙에 새로운 요소가 추가될 경우, 완전 이진 트리를 유지하기 위해 항상 트리의 마지막 노드에 추가한다.
- 부모 노드와 비교해가며 클 경우에 자리를 바꾼다.
- 더 이상 비교할 부모가 없을 경우 삽입 연산을 종료한다.
그림으로 알아보기 (최대 힙)
1. 힙에 새로운 요소가 추가될 경우, 완전 이진 트리를 유지하기 위해 항상 트리의 마지막 노드에 추가한다
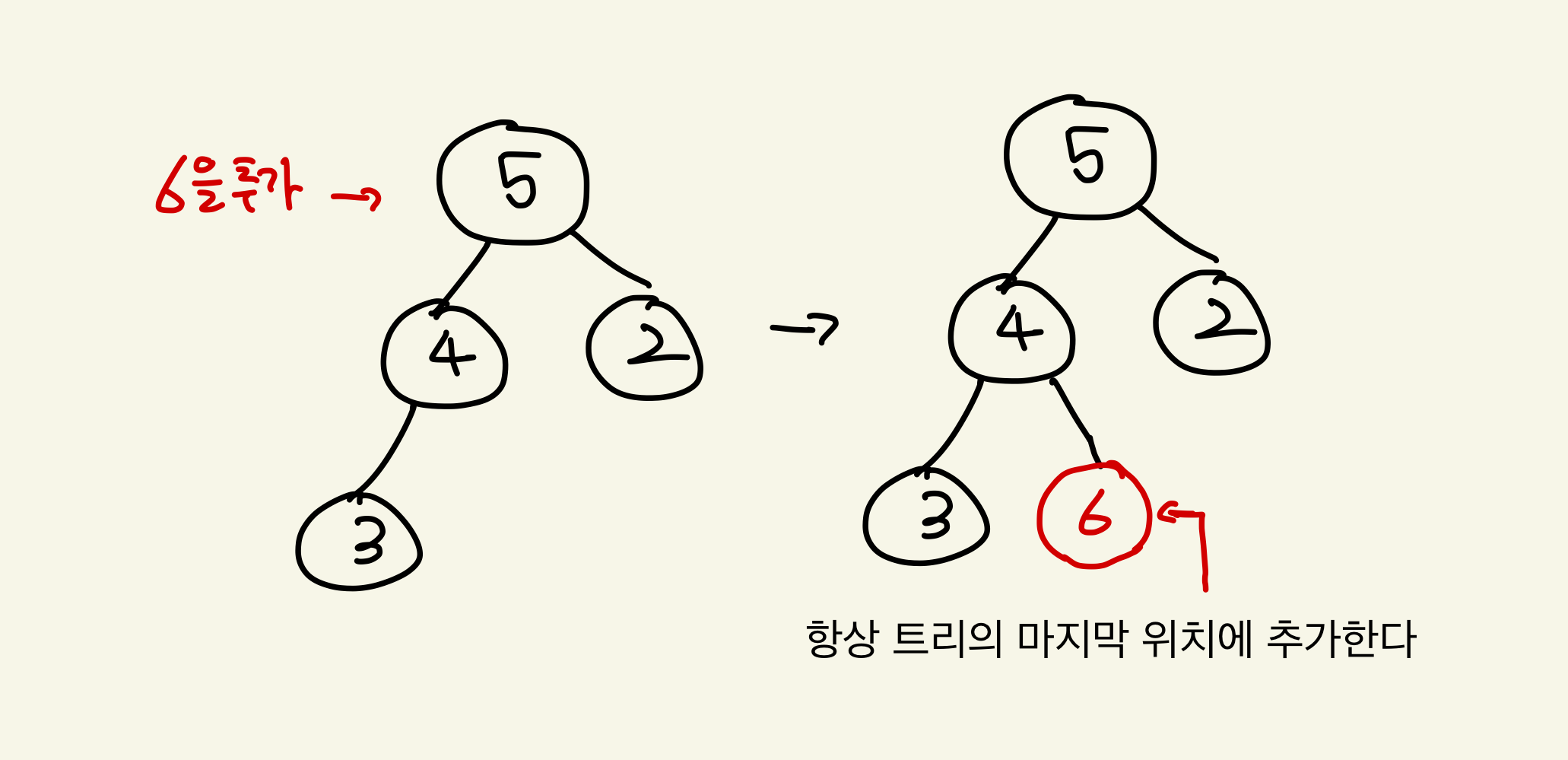
2. 부모 노드와 비교해가며 클 경우에 자리를 바꾼다.

3. 더 이상 비교할 부모 노드가 없는 경우 삽입 연산을 종료한다.

힙의 삽입 연산은 완전 이진 탐색의 마지막 노드에 추가하기 때문에, 트리 배열의 마지막 인덱스에 추가해주면 된다. 따라서 삽입 그 자체는 원타임 O(1) 에 이루어진다. 삽입 이후 부모 노드와 비교하는 작업을 진행하는데, 완전 이진 탐색이기 때문에 트리의 높이만큼 비교 연산을 진행하게 된다. 완전 이진 트리의 높이는 log N 이므로 최종적으로 삽입 연산의 시간 복잡도는 O(log N) 이 된다.
힙의 삭제 연산 - 시간 복잡도 (log N)
- 힙은 우선순위가 제일 높은 데이터가 먼저 나간다. 이 때 우선순위가 제일 높은 데이터는 항상 루트 노드에 존재하므로, 루트 노드의 데이터를 바로 리턴한다.
- 완전 이진 트리를 유지하기 위해 트리의 마지막 노드를 부모 노드로 옮긴다.
- 왼쪽, 오른쪽 자식 노드와 비교해가며 우선 순위가 자기보다 높은 노드와 자리를 교환한다. 만약 왼쪽, 오른쪽 전부 자기보다 우선 순위가 높으면 더 높은 쪽과 교환한다.
그림으로 알아보기 (최대 힙)
1. 힙은 우선순위가 제일 높은 데이터가 먼저 나간다. 이 때 우선순위가 제일 높은 데이터는 항상 루트 노드에 존재하므로, 루트 노드의 데이터를 바로 리턴한다.
2. 완전 이진 트리를 유지하기 위해 트리의 마지막 노드를 부모 노드로 옮긴다.

3. 왼쪽, 오른쪽 자식과 비교해가며 우선 순위가 자기보다 높은 자리를 교환한다.

힙의 삭제 연산 또한 데이터 삭제는 원타임 O(1) 에 이루어지고, 자식 노드랑 계속해서 비교하므로 트리의 높이만큼 비교연산을 수행한다. 따라서 삭제 연산의 시간 복잡도는 O(log N)이 된다
힙의 구현
- 힙은 완전 이진 트리이므로, 배열로 구현하는게 제일 편리하다. 왼쪽 자식 노드는 부모 인덱스 * 2 가 되고, 오른쪽 자식 노드는 부모 인덱스 * 2 + 1 으로 바로 찾아갈 수 있기 때문이다.
- 힙의 삽입과 삭제연산 중 부모, 자식 노드와 비교하고 교환하는 연산을 수행할 때, 노드를 교환하기 보다는 데이터 그 자체만 스왑하는 편이 구현이 훨씬 간단하다.
- 삭제 연산도 마찬가지로 루트 노드와 자식 노드의 연결을 끊어버리면 트리의 구조가 완전히 무너지게 되므로, 데이터만 반환한 뒤 제일 마지막 노드의 데이터를 가져온다
배열로 표현하기
static int[] heap = new int[100001]; //힙 (완전 이진 트리)
static int heapSize = 0; //트리의 크기힙의 삽입 연산
삽입
static public void add(int data) {
heap[++heapSize] = data; //트리의 마지막 노드에 데이터를 추가한다.
pushPostfix(heapSize); //삽입 후처리 연산
}삽입 후처리
static private void pushPostfix(int index) {
//부모 노드가 존재하고, 부모 노드보다 우선순위가 높을 경우
while (index > 1 && heap[index / 2] < heap[index]) {
swapNode(index, index / 2); //부모 노드와 데이터만 교환한다.
index = index >>> 1;
}
}
힙의 삭제 연산
삭제
int poll() {
int ret = arr[1]; //반환값은 루트 노드
arr[1] = arr[heapSize]; //루트 노드 데이터를 마지막 노드의 데이터로 지정
arr[heapSize--] = -1; //마지막 노드는 삭제한다.
int cur = 1; //루트 노드부터 자식 노드와 비교 시작
//자식 노드가 존재하면
while ((cur << 1) <= heapSize) {
//왼쪽 자식 노드가 오른쪽 보다 더 큰지?
boolean leftBig = compare(cur << 1, (cur << 1) + 1);
//왼쪽 자식노드가 오른쪽 자식 노드보다 더 크고, 자기보다 더 크다면 교환
if (leftBig && compare(cur << 1, cur)) {
swap(cur, cur << 1);
cur <<= 1;
}
//오른쪽 자식노드가 왼쪽보다 더 크고 자기보다 더 크면 교환
else if (!leftBig && compare((cur << 1) + 1, cur)) {
swap(cur, (cur << 1) + 1);
cur = (cur << 1) + 1;
}
//왼쪽 오른쪽 모두 자기보다 더 작으면 교환하지 않고 연산을 종료
else {
break;
}
}
return ret;
}